第9回 | 仕様のはなし | コイルを使う人のための話(第2部)

第9回 | 仕様のはなし

概算値を知る

あるインダクタンスから別のインダクタンスに変えた場合に、インダクタンス以外の特性がどの程度変化するのか、概算値で良いので知りたいことがあります。

もちろん、インダクタの仕様一覧をみれば直ぐに分かることですが、一覧表が無くても概算値（正式な値ではありません）を簡単な計算で知ることができます。

実際の概算値の計算方法ですが、次のような変換を行います。

※インダクタンス値がk倍（k = 知りたいインダクタンス／既知のインダクタンス）になると、
　　→ 直流抵抗値は、インダクタンスと同様にk倍になります。
　　→ 直流重畳電流は、1/√k倍になります。
　　→ 温度上昇電流は、1/√k倍（直流抵抗がk倍になるので）になります

なぜ、このような計算式で概算値が求められるのかは、一般のインダクタの場合には次のような関係があるからです。

1. インダクタンス値は、巻数の二乗に比例する（インダクタンスの計算式参照）。
   → 巻数が2倍になると、インダクタンス値は4（ = 2²）倍になる。
2. 同一形状（構造）の場合、電流値×巻数の値(アンペア・ターン)は一定。
   → 巻数が2倍になると、直流重畳電流は1/2倍になる。
3. 巻線する巻溝部分の占有率は、インダクタンス値に関係無く一定で均一。
   → 電線径が2倍になると、最大巻数は1/4（ = 1/2²）倍になる。

実際のインダクタの場合は、100%上記の関係を満たしている訳ではないので、計算式で得られる値も誤差を含みますから概算値になります。

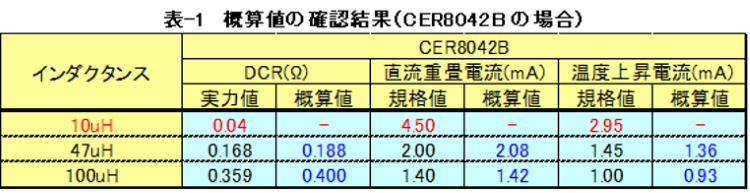
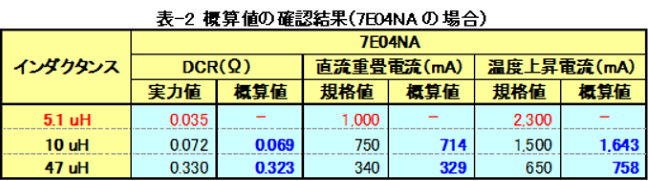
実際に、弊社のパワーインダクタCER8042Bの仕様で確認した内容を表-1に、7E04NAの仕様で確認した内容を表-2に示します。

確認方法は、一番上のインダクタンスの規格値（または実力値）を基準（赤字）にして、残りのインダクタンスの概算値（青字）を求めて比較してみました。

形状やインダクタンスによりバラツキも有りますが、先ずは概値として利用できる範囲だと思いませんか？

特性グラフの場合

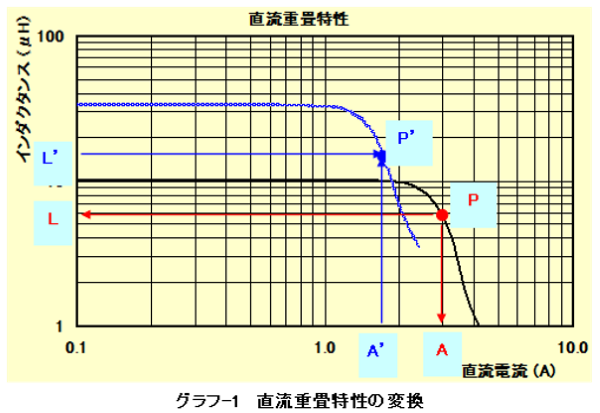
グラフ-1のような直流重畳特性があり、例えば10μHの特性曲線（黒線）しかなかったとしても、他のインダクタンスの直流重畳特性の値を知ることができます。

方法は簡単で、例えば、33μHの特性が知りたい場合は、次のように行います。

1. 10μHのグラフ上のP点の電流値AとインダクタンスLを読み取ります
2. 電流値A’=A×√10/33、インダクタンスL’=L×√33/10を求めます。
3. A’とL’で示される点、P’をプロットします。
4. P点の位置を変えて、P’をプロット（青線）していきます。

あるいは、10μHでインダクタンスが30%低下するときの電流値Aを求めれば、33μHでインダクタンスが30%低下する電流値は、A’=A×√10/33で求めることができます。

周囲温度とコイルの発熱（ΔT）

周囲温度が常温（例えば+20℃）の時のコイルの発熱ΔT（全て直流電流による発熱とする）が分かれば、周囲温度が上昇した時のコイルの発熱ΔT’（常温時と同じ直流電流とします）の概算値を計算で知ることができます。

コイルに使用している銅線の直流抵抗値は、プラスの温度係数を持っていますので、周囲温度が上がるとコイルの直流抵抗も増加し、コイルの電流値が変わらなくても発熱は増加します。

従って、周囲温度が上昇したときの発熱は、この抵抗値の増加も考慮する必要がありますが、ここでは結果だけを示します。

常温T0（例えば+20℃）の時のコイルの発熱をΔT0 とし、周囲温度がTaのときの発熱ΔTa の概算値は、次の式で求めることができます。なお、銅線の直流抵抗の計算が関係するので、0.92や0.004と言った数値が出てきます。

ΔTa ≈ 0.92 × ΔT0 + (0.92 + 0.004 × (ΔT0 + T0)) × Ta - Ta

あるいは、10μHでインダクタンスが30%低下するときの電流値Aを求めれば、33μHでインダクタンスが30%低下する電流値は、A’=A×√10/33で求めることができます。

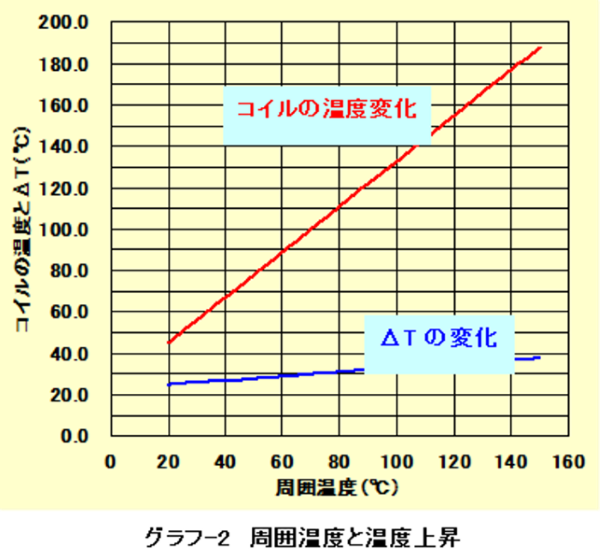
グラフ-2は、周囲温度T0が20℃のときにΔT0 = 25℃のコイルを、周囲温度を上昇させたときの温度変化（赤線）と温度上昇ΔTa（青線）の変化を示したものです。

周囲温度の上昇と共に、ΔTも増加することは、回路の損失が増加することを意味します。

従って、周囲温度ができるだけ上がらないようにすることは、電源回路の場合は変換効率を低下させないことを意味します。

利用上のお願い

今回お話しした内容は、理想状態を想定（求める特性に関係無い項目は無視します）して計算してあります。

従って、実際と必ずしも一致しない場合もありますので、あくまでも概算を知るための方法と思って下さい。

また、製品の構造・その他の要因により、概算値が大きく異なる場合も有ります。

写真-2のような場合も、コイルの構造が特殊なので、うまく概算が求められない可能性が大きいです。

著者紹介

• 本文中に掲載の製品の一部には、既に生産が終了しているものが含まれている場合がございます。
• 記事作成から時間が経過しているので、記載の情報が古いままの内容が含まれている場合がございます。